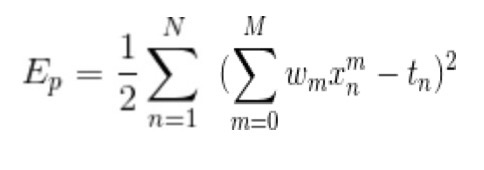1주차 되짚기
앞선 1주차 글에서는 머신러닝의 기법들에 대해서 간단히 알아보았는데, 이러한 머신러닝 기법들은 어떻게 발현되고 어떠한 원리를 통해 이루어지는 것 일까? 기계를 학습시키는 머신러닝을 하기 위해서는 수학적인 접근이 필요하다. 앞서 말했던 기법들을 이해하기 위해서는 그 속을 이루는 수학적인 식, 원리를 이해해야한다. 물론 나도 문과생을 대상으로 쓰는 글이고, 본인도 문과생이기에 수학적인 내용을 더 강조해주고 싶다.
< Elice Academy - 문과생을 위한 머신러닝 > https://academy.elice.io/courses/544/lectures/3842
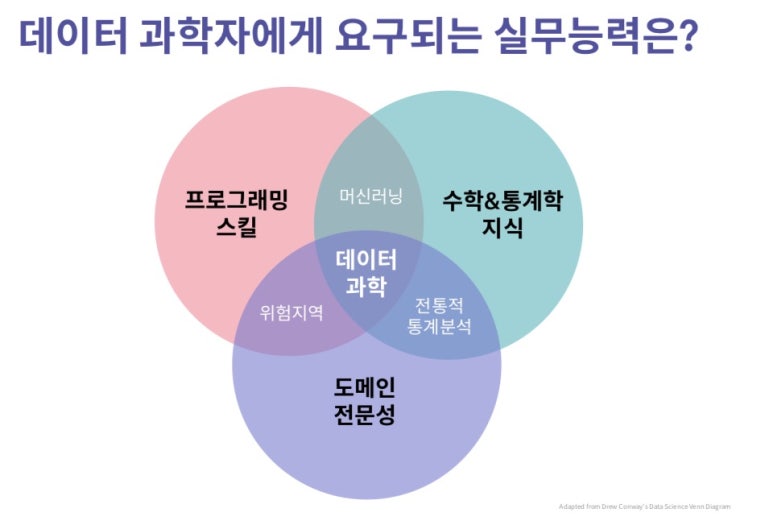
앞선 내용에서 봤던 세 가지 분야이다. 문과생이 이 세 가지 분야에서 어느 부분이 가장 약할 거 같은지는 딱 보면 알 수 있다. 바로 수학&통계학 지식이 제일 떨어질 수 밖에 없다. 하지만 머신러닝을 위해서, 혹은 머신러닝에서 더 나아간 데이터 사이언스를 하기 위해서는 수학이 필수적으로 수반됨을 알 수 있다. 고등학교 졸업 이후 거의 대부분이 수학에 손을 떼고, 거리를 두고 살아가고 있을 것 이다. 나도 그랬고 주변도 그런 모습을 보이고 있다. 하지만 머신러닝을 공부하고 싶은 문과생이라면 수학적인 지식이 필요하다는 것을 인지하고! 조금 오래걸릴지라도 머신러닝이 요구하는 수학적 지식을 겸비하는 것이 바람직 할 것이다.
수학, 어디서부터 시작해야 할까?
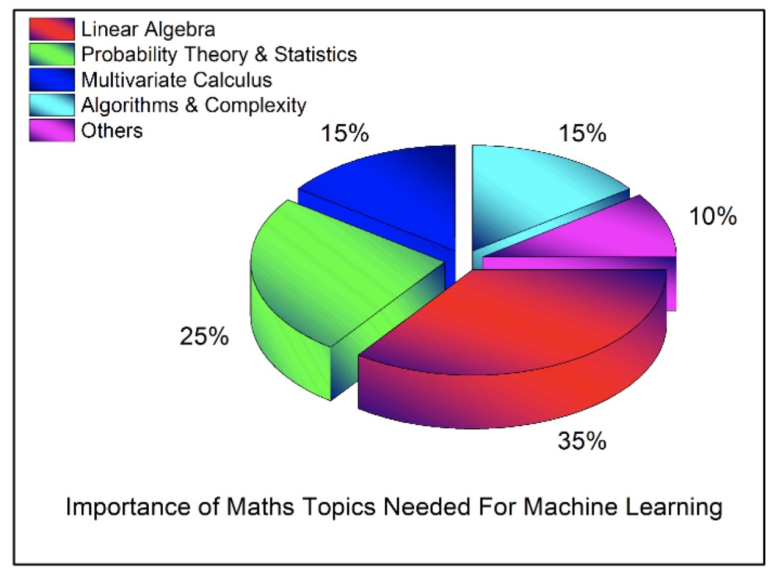
수학이 계속 필요하다고 말하고 있는데 이를 보고 막상 시작하려한다면 막막할 것이다. 그래서 간략하게 수학&통계에서도 어느 부분을 집중적으로 해야 할지 말해주고 싶다. 무조건 이대로 하라는 것은 아니고 자기가 필요하다고 생각하는 부분을 심화 하던가, 참고하는 정도로만 이용하는 것이 좋을 것 같다. ( 원래 굉장히 복잡한 분야이지만 간단하게 어느정도가 있는지만 짚어볼 것 이다. )
< 머신러닝에서 요구되는 각 수학분야의 중요성 >
선형대수학 (Linear Algebra)
선형대수학(linear algebra)은 벡터 공간, 벡터, 선형 변환, 행렬, 연립 선형 방정식 등을 연구하는 대수학의 한 분야이다. 현대 선형대수학은 그중에서도 벡터 공간이 주 연구 대상이다.
▶ 주성분 분석 (Principal Component Analysis, PCA)
▶ 단일값 분해 (Singular Value Decomposition, SVD)
▶ 행렬의 고유분해 (Eigendecomposition of a matrix)
▶ LU 분해 (LU Decomposition)
▶ QR 분해 (QR Decomposition/Factorization)
▶ 대칭 행렬 (Symmetric Matrices)
▶ 고유값 & 고유벡터 (Eigenvalues & Eigenvectors)
▶ 벡터 공간과 노름 (Vector Spaces and Norms)
확률과 통계
▶ 조합 (Combinatorics)
▶ 확률 규칙 및 공리 (Probability Rules & Axioms)
▶ 베이지안 이론 (Bayes’ Theorem)
▶ 랜덤 변수 (Random Variables)
▶ 분산과 기댓값 (Variance and Expectation)
▶ 조건부 확률 및 결합 확률 분포 (Conditional and Joint Distributions)
▶ 표준 분포 (Standard Distributions)Bernouil
▶ Binomial
▶ Multinomial
▶ Uniform
▶ Gaussian
▶ 모멘트 생성 함수 (Moment Generating Functions)
▶ 최대 우도 추정 (Maximum Likelihood Estimation, MLE)
▶ 사전 및 사후 확률 (Prior and Posterior)
▶ 최대 사후 추정 (Maximum a Posteriori Estimation, MAP)
▶ 샘플링 방식 (Sampling Methods)
미적분학
▶ 미분 및 적분 (Differential and Integral Calculus)
▶ 편미분 (Partial Derivatives)
▶ 벡터값 함수 (Vector-Values Functions)
▶ 방향 그라디언트 (Directional Gradient)
▶ Hessian
▶ Jacobian
▶ Laplacian
▶ Lagrangian 분포 (Lagrangian Distribution)
Linear regression "최소제곱법" 사례
일단 한 분야에만 속하는 알고리즘이 존재하는 것이 아니기 때문에 간단한 사례를 통해 알아보자. 가장 대표적인 linear regression에서만 해도 선형대수학의 벡터,행렬 미적분학의 Hessian, 편미분 등등의 개념이 등장한다. 이를 간단하게 알아보자
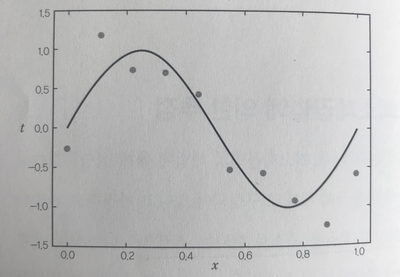
그냥 코딩으로만 linear regression을 해봤던 사람이라면 어떠한 원리를 통해 예측하는지 모를 것이다. inear regression에서는 "최소제곱법"이라 불리는 개념이 쓰인다. 이 기법안에는 머신러닝 이론의 기초가 되는 '통계 모델'의 사상이 응축되어 있기도 하기 때문에 "최소제곱법"을 아는 것은 매우 중요하다. 최소제곱법이란 어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다. 한 번 수학적인 시각으로 바라보자.
< 최소제곱법을 통해 추정된 선 >
저 선은 오차의 제곱을 최소로 한다는 조건으로 만들어진 선이다. 먼저 x를 설명변수 t를 목적변수라고 칭하고 시작해보자.
x와 t의 함수관계는 다음과 같이 표시할 수 있다.
(2.1)
이 함수에 대한 오차식은 다음과 같이 표시할 수 있다.
(2.2)
10군데의 각 지점에 있는 t값과 t_n의 값의 차분을 제곱하고 총합을 구하는 것이다.
오차값이 크다는 이야기는 식 2.1로 추정되는 t값이 실제 관측된 t_n의 값과 유사하지 않다는 의미가 된다. 하지만 오차값이 가능한 작아질 수 있도록 하는 파라미터
(2.22)
을 찾아낸다면 관측값 t_n이 t값과 비슷해질 것이라고 이야기 할 수 있다.
이후 간단한 계산을 위해 2.2 식을 1/2한 값을 오차 Ep라고 정의할 것 이다.
(2.3)
위 그림에서는 N이 10이지만 관측점 개수가 달라졌을 때도 적용될 수 있게 N으로 표기하였다. 2.2를 최소로 하는 조건이나 2.3을 최소로 하는 조건 중 어느 것을 사용하던 같다. 그렇다면 2.3에 2.1을 대입한 결과는 아래와 같다.
(2.4)
결국에는 2.4의 식의 값인 Ep를 최소로 만드는 것이 최소제곱법의 최종 목표이다.
보통 2.3으로 계산되는 오차를 일반적으로 '오차의 제곱'이라고 부른다. 우리는 오차의 제곱을 최소화 할 수 있는 답을 구하려고 하는 것이기 때문에 이를 '최소제곱법'이라고 말하는 것이다!
앞서 말했을 때는 벡터와 행렬, 미적분학이 쓰인다고 그랬는데 다음을 보면 알 수 있다.
아까 2.4를 최소로 만드는
를 찾아보는 과정에서 알 수 있다. 이것은 2.4를 2.22에 대한 함수로 간주하여 편미분계수가 0이 된다는 조건을 적용시켜 찾는 것이다.여기서 일단 편미분이 등장하게 된다. 문과생이라면 편미분이 매우 생소한 개념으로 다가설 것 이다. 간단히 말하자면 한 함수에 대해 하나의 변수에 대해 미분한다는 것이다. 나머지는 그저 변수가 아닌 상수로 보고 진행하는 것이다.
(2.5)
m은 0, ~~ M까지 이다.
계수를 모두 합쳐서 벡터
라고 지정하면 기울기 벡터가 0이 된다고 말해도 된다. 세로벡터를 사용하기 때문에 T가 붙어있음을 알 수 있다. 벌써 지금까지만 봐도 모르는 부호들, 개념들이 많이 등장한다. 여기까지만 읽어도 아.. 수학해야겠다라는 생각이 많이 들 것이다. 그런 생각이 들었다면 일단 이 글은 성공한 것 같다. 아무튼 그래서
(2.6)
이라는 식이 나오게 되는 것이다. 2.5식에 2.4를 대입하여 편미분을 계산하면 아래돠 같은 식이 얻어진다. 식이 헷갈리지 않게 2.4의 m을 m'로 표기하는게 보기 좋을 것이다.
(2.8)
굉장히 골머리아픈 식이 하나 보이는 것 같을 것이다. 이것을 좀 더 간단히 정리하자면 x_n^m을 (n,m)의 원소로 구성된 Nx(M+1) 행렬 A를 만들면 행렬식으로 변환이 가능하다.
(2.9)
w는 앞서 정의한 그대로고 우리가 구해야 할 계수를 나열한 벡터를 의미한다.
t는 목적변수의 관측값을 나열한 벡터 t이다. A같은 경우는 N개의 관측점에 대해 각각을 0~M제곱한 값을 나열한 행렬이다.
(2.10)
이제 이 행렬을 변형해서 계수 w를 구할 수 있게 된다. 2.9의 양변을 전치하면 아래와 같은 결과를 얻는다.
(2.11)
A와 t의 정의를 다시 보면 이들은 트레이닝 셋에 포함된 관측 데이터에 의해 정해지는 값들이다. 즉 2.11은 주어진 트레이닝 셋을 사용하여 다항식의 계수 w를 결정하는 공식이라고 말할 수 있다. 이제까지는 Ep의 편미분계수가 0이되는 즉 Ep가 극값을 취할 조건만으로 계산을 진행했다. 하지만 2.11에 A^T A의 역행렬이 포함되어있는데 이것이 확실하게 역행렬을 갖는지도 알아야 한다.
그렇다면 여기서 Ep의 2계 편미분계수를 나타내는 헤세행렬을 사용한다. (모르는 단어들이 계속 나오는 것을 보며 수학의 필요성을 느꼈으면..) 헤세행렬 H는 (M+1)x(M+1)인 정방행렬이다.
(2.12)
Ep의 정의 식 2.4를 위의 식에 대입하면 아래와 같은 식을 얻을 수 있다.
(2.13)
식 2.10을 사용하면 2.11로 역행렬을 취하는 부분에 있는 행렬이 헤세행렬과 일치한다는 것을 알 수 있다.
(2.14)
이 때 M+1 <= N 즉 계수의 개수인 M+1이 트레이닝 셋 데이터의 개수 N 이하라면 헤세행렬은 양정치라는 것을 알 수 있다. 양정치라는 것은 임의의 벡터 0이 아닌 u에 대해 u^T Hu >0 가 성립하는 상태를 말한다.
반대로 M+1 > N으로 계수의 개수가 트레이닝 셋의 데이터 개수보다 클 때에는 헤세행렬이 반양정치가 된다. 따라서 Ep를 최소로 만드는 w가 여러 개 존재하게 되어 하나의 값으로 정해지지 않는다.
정말 간단하게 linear regression의 원리인 "최소제곱법"에 대해 알아 봤는데 느낀 것이 많을 것 이다. 먼저 프로그래밍으로만 알던 사람은 선형회귀선을 만드는데 이러한 원리가 있다는 것에 놀랐을 것이고 문과생들은 식만 보고도 충분히 놀랐을 것이다. 위 같은 사례를 보여준 이유는 정말 간단한 알고리즘이라고 생각되는 방식이지만 그 속에는 많은 수학적인 지식이 내포되어 있다는 것을 말해주고 싶었다. 나도 이러한 과정을 통해서 수학의 중요성을 깨닫고 천천히 거북이처럼 하나하나 공부해가고 있다. 문과생이라면, 혹은 수학적 지식이 조금 부족하다면 천천히 수학적 지식을 확장시키는게 추후에 매우 도움이 될 것이라고 생각한다.
수학은 필수이지만 그 전에 도메인 지식이나 머신러닝을 수학이 아니라 쉽게 접하고 싶다면 아래 강의를 듣는 것도 괜찮을 것 같다.
수학적 지식을 다루고 있지는 않지만 머신러닝에 대한 전반적인 이해를 돕는데 괜찮을 것 같다. 맨 처음에 말했던 세 분야에서 중요성이 떨어지는 것은 없지만 각자 한 분야를 날카롭게 만들어 자기만의 강점으로 가지고 있는 것이 도움이 많이 될 것이라고 판단된다. 굳이 수학을 선행하라는 말은 하지 않지만, 선행될 경우 추후에 배우는 것들을 이해하는데 큰 도움이 될 것 같다. 마무리 하면서 수학을 어려워하는, 꺼려하는 사람들도 다 할 수 있다고 말하고 싶다. 나도 중고등학교때 수학을 많이 싫어했지만 대학에 와서 목표의식이 생기고 그 과정에 수학이 포함되어 있다는 것에 꺼렸지만, 의지만 있다면 누구나 다 할 수 있을 것이다!
참조글 : https://mingrammer.com/translation-the-mathematics-of-machine-learning/
참조서 : [머신러닝 이론 입문]