[Swift] Binary Search Tree란? (1)

Binary Search Tree는 (하나의 node가 최대 2개의 자식을 갖는) 트리가 항상 정렬되도록 추가/삭제를 수행하는 binary tree의 한 종류이다.

 

"항상 정렬되어 있다"의 의미는 무엇일까?

 

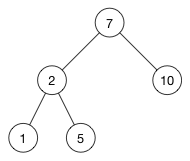
위 트리를 봐보자. 

 

- parent node : 7

- left child : 2 

- right child : 10

 

node를 기준으로 좌측의 키는 항상 작아야 하며, 우측의 키는 항상 커야한다. 그렇기에 각각의 child들은 정렬되어 있을 수 밖에 없는 것이다. (child의 child 또한 마찬가지)

 

Insert

 

그렇다면 기존 트리에 새로운 node를 추가할 때는 어떻게 해야할까? 

먼저 새로운 node 값을 추가할 때 roott node(최상단)의 값과 비교한다. 만약 새로 추가하고자 하는 값이 더 작을 경우 왼쪽 branch로 보내고, 클 경우 오른쪽 branch로 보내게 된다. 계속 트리를 내려가면서 값을 비교하며 더 이상 비교할 수가 없을 때 해당 위치에 새로운 값을 추가한다. 

 

예를 들어 "9"를 넣고 싶다라고 가정해보자. 

 

- 9는 7(root)보다 크다. -> 우측 branch로 이동

- 9는 10보다 작다. -> 왼쪽 branch로 이동한다. 

 

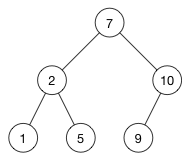
쭉쭉 내려오면서 비교하면서 빈 자리를 찾기 때문에 시간 복잡도는 O(h)이다. ( h = 트리의 높이, 높이는 root부터 가장 밑단의 leaf 까지의 거리를 의미한다. )

 

그냥 간단한 룰을 따르면 된다! 작은 수는 좌측에, 큰 수는 우측에! 항상 트리를 정렬시켜두기 때문에 트리 내에 값이 있는지 잘 확인할 수 있다. 

 

Search

 

그렇다면 트리 내에서 값을 찾고자 할 경우는 어떻게 해야할까? 추가할 때와 동일한 step으로 진행된다. 

 

- 값이 현재 node 보다 작을 때, 좌측 branch로 

- 값이 현재 node 보다 클 때, 우측 branch로

- 값이 현재 node와 같을 때, 원하는 값을 얻게 되는 것이다!

 

값을 찾을 때 까지 주로 재귀적으로 수행된다. 

5를 찾는 경우를 봐보자. 

 

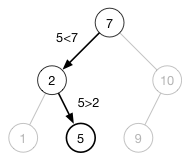
검색 또한 마찬가지로 O(h)로 빠른 속도를 보인다. 만약 100만 개의 노드로 이루어져 있고 균형이 잘 잡힌 트리가 있을 경우, 오직 20 step이면 트리에 있는 어떤 값이든 찾아낼 수 있다. ( 배열에서의 Binary Search의 개념과 유사하다! )

 

Traverse

가끔은 하나의 노드가 아니라 모든 노드들을 봐야할 필요가 있다. 

이럴 경우, binary tree를 순회(traverse)하는 세 가지 방법이 있다. 

( 모든 순회 방식은 재귀적이다 )

 

1. In-order (or depth-first)

 

node의 좌측 끝 child를 맨 처음 보고, 해당 node를 보고, 오른쪽 child로 이동하여 계속 순회한다. 

 

https://gnujoow.github.io/ds/2016/09/01/DS4-TreeTraversal/

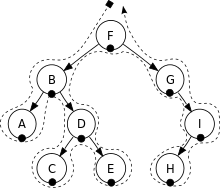
순회 순서 : A > B > C > D > E > F > G > H > I

                (C와 H 차례인 이유는 그 상황에서 가장 좌측 끝에 있는 child이기 때문!)

 

2. Pre-order

 

node를 먼저 보고 좌, 우 child를 본다. 

 

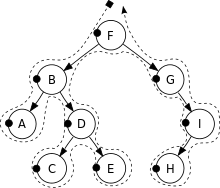
순회 순서 : F > B > A > D > C > E > G > I > H

 

3. Post-order

 

먼저 좌, 우 child를 보고 node를 제일 마지막에 본다. (child를 우선적으로 보는 것!)

 

순회 순서 : A > C > E > D > B > H > I > G > F

 

 

Delete

node들을 제거하는 것은 쉽다. node를 지우고 나서, 해당 위치에는 좌측 child 값 보다 크고 우측 child 값 보다 작은 값으로 대체되어야 한다. 그래서 node를 제거한 이후에도 트리는 정렬되어 있게 되는 것이다. 아래 예시를 보면 10은 제거되었지만 9나 11로 대체된 것을 볼 수 있다. 

 

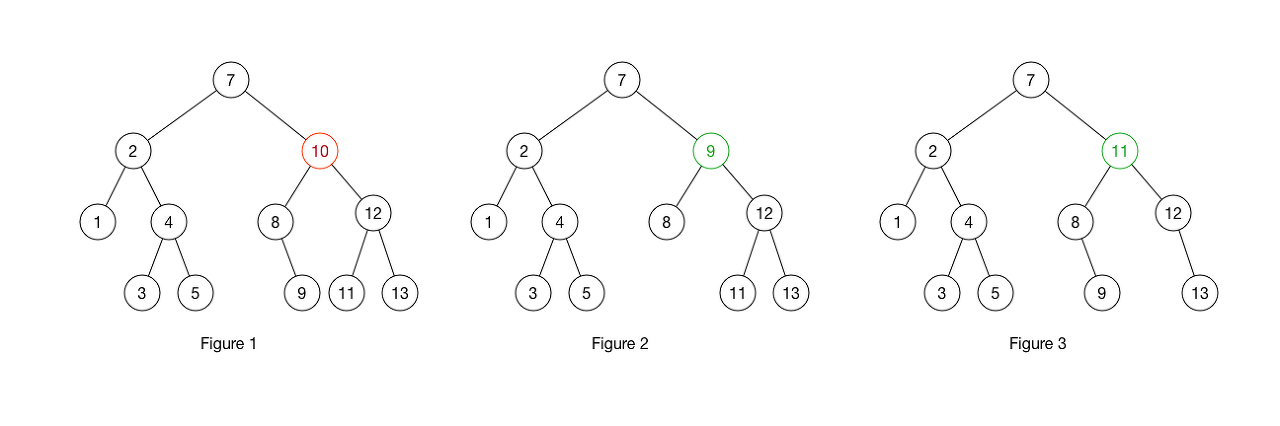
자식이 없은 leaf node들은 그냥 끊어내면 된다!

 

다음 게시글에서 이어서 코드로 어떻게 구현하는지 살펴보자!