![[프로그래머스] 가장 먼 노드 (with BFS)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FFCQOG%2Fbtq250qheOu%2F2YUF1ABTWP0MDRnqi66l1K%2Fimg.png)
programmers.co.kr/learn/courses/30/lessons/49189?language=swift
코딩테스트 연습 - 가장 먼 노드
6 [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] 3
programmers.co.kr
문제 제목 그대로 1번 노드에서 가장 먼 노드를 구하는 문제!
바로 문제의 예시를 봐보자.
음.... 그래프를 보니 최근에 배웠던 플로이드-와샬을 써보고 싶어진다.. 그래서 써봤다.. 당연히 시간초과..
문제의 "제한사항"을 잘 봐야한다!
- 노드의 개수 n은 2 이상, 20,000 이하입니다.
플로이드-와샬의 시간 복잡도는 $O(n^3)$ 이었으니까... 딱 봐도 안된다..
이렇게 "간선"에 가중치가 없고 양방향인 경우에는 BFS (Breadth-First-Search) 즉, 너비 우선 탐색 기법을 통해 해결할 수 있다.
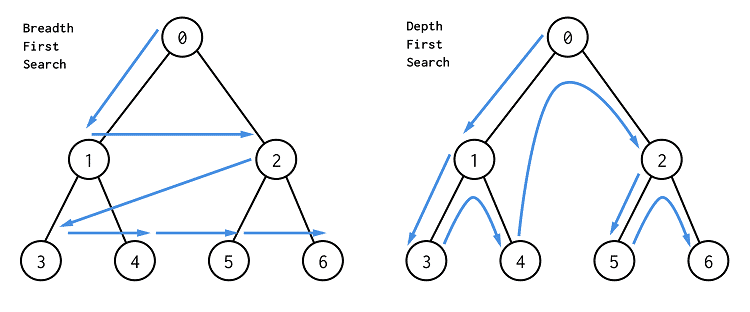
말 그대로 깊이가 아닌 너비를 우선으로 탐색을 하는 것이다. 왼쪽부터 하던, 오른쪽 부터 하던 상관은 없다!
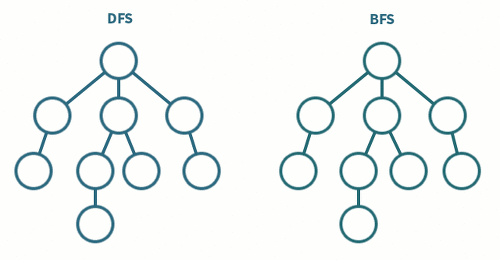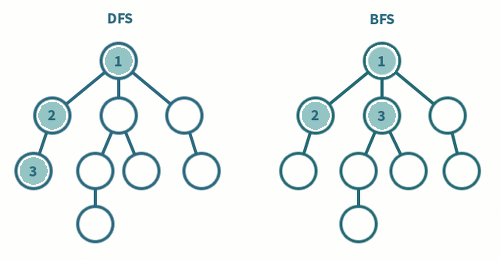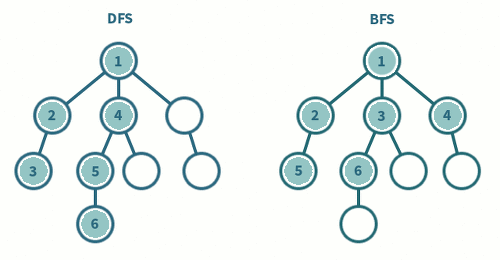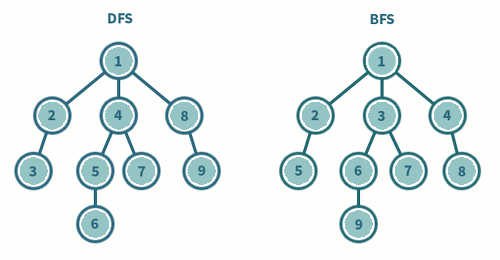
다만 이 문제를 DFS로 풀게 되면 오류가 발생하게 되는데, DFS는 깊이를 우선으로 탐색하기 때문이다.
즉 가까운 거리를 놔두고, 굳이 멀리멀리 가버릴 수 있다는 것이다.
만약 주어진 연결정보가 (1,2) (1,3) (2,3) 이었다고 해보자.
DFS로 탐색했을 때는 3이 2와 같은 레벨에 있음에도...! 1부터 3까지의 거리는 2라는 결론을 내리게 된다.
(DFS : 1 > 2 > 3, BFS : 1 > 2, 3)
이에 DFS로 제약 사항을 걸어주지 않는 이상, 최적의 경로를 찾아주는 BFS를 택하는 것이 바람직해보인다.
아무튼 이제 다시 문제로 돌아와보자.
해야할 task는 가장 멀리 떨어진 노드의 거리를 찾고, 가장 멀리 떨어진 노드의 개수를 세서 리턴해주면 된다.
코드로 보면서 이해해보기 전에 직접! 문제의 예시를 손으로 한 번 그려보자.
우선 연결정보를 먼저 담아준다.
// n = 6
// vertex = [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]
// [Int:[Int]] 형태로 저장해준다.
// 예
var nodes = [1:[2,3], 2:[1,3,4,5], 3:[1,2,4,6], 4:[2,3], 5:[2], 6:[3]]각각 노드(key) 인접한 노드들을 value에 담아줬다.
시작점은 1이기 때문에 초기화해주고 시작해야한다. (자기 자신이기에 거리는 0)
Step 1.
초기 세팅은 아래와 같다.
갑자기 등장한 visited는 해당 노드를 이전에 방문했었는지 여부를 확인해주는 역할을 한다. 이전에 들렀으면 굳이 또 들를 필요가 없다는 것이다!
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | F | F | F | F | F | F |
| depth | - | - | - | - | - | - |
인접 노드로의 안내를 하기 위한 queue와 결과를 보존하기 위한 result를 선언하여 알맞게 저장하고 추출해준다.
자 여기서 자기 자신에서 출발할거라는 정보를 넣어준다.
| i | queue | result |
| 1 | (1,0) | (1,0) |
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | F | F | F | F | F |
| depth | 0 | - | - | - | - | - |
Step 2.
step 이동시 마다, queue에서 removeFirst하여 원소를 하나 빼낸다. 해당 원소를 (key,depth)라고 해보자. 그리고 nodes[key]!를 통해 현재 연결되어 있는 인접 노드들의 리스트를 가져온다. 인접 노드로 이동할 것이기에 depth는 이전 노드의 depth를 기준으로 1씩 추가해준다.
지금은 2와 3이 인접해 있어 해당 값들을 가져올 수 있다.
2의 경우부터 보자. (순서 무관)
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | F | F | F | F | F |
| depth | 0 | - | - | - | - | - |
2는 아직 방문하지 않았다. 즉 탐색의 자격이 충족된다!
탐색함과 동시에 T로 바꿔주고, depth를 입력해준다.
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | T | F | F | F | F |
| depth | 0 | 1 | - | - | - | - |
| i | queue | result |
| 1 | [(1,0)] | [(1,0)] |
| 2 | [(2,1)] | [(1,0),(2,1)] |
queue의 FIFO 특성을 이용해 원소들을 뽑는다.
3도 동일한 과정을 반복해준다.
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | T | T | F | F | F |
| depth | 0 | 1 | 1 | - | - | - |
| i | queue | result |
| 1 | [(1,0)] | [(1,0)] |
| 2 | [(2,1)] | [(1,0),(2,1)] |
| 3 | [(2,1),(3,1)] | [(1,0),(2,1),(3,1)] |
Step 3.
자 이제 또 현재 queue에서 removeFirst 하여 (2,1)이 나오게된다. 그렇다면 이제는 2와 인접한 노드들을 탐색해줘야한다.
2와 인접한 노드는 [1,3,4,5]이다.
자 여기서 visited가 핵심적인 역할을 해준다.
1과3은 이전에 이미 들린 기록이 있다. 이럴 경우 해당 경우는 스킵해주면 된다.
즉 인접노드 [4,5]에 대해서만 확인해주면 된다.
4를 먼저 봐보자.
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | T | T | T | F | F |
| depth | 0 | 1 | 1 | 2 | - | - |
| i | queue | result |
| 1 | [(1,0)] | [(1,0)] |
| 2 | [(2,1)] | [(1,0),(2,1)] |
| 3 | [(2,1),(3,1)] | [(1,0),(2,1),(3,1)] |
| 4 | [(3,1),(4,2)] | [(1,0),(2,1),(3,1),(4,2)] |
5도 탐색해주자.
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | T | T | T | T | F |
| depth | 0 | 1 | 1 | 2 | 2 | - |
| i | queue | result |
| 1 | [(1,0)] | [(1,0)] |
| 2 | [(2,1)] | [(1,0),(2,1)] |
| 3 | [(2,1),(3,1)] | [(1,0),(2,1),(3,1)] |
| 4 | [(3,1),(4,2)] | [(1,0),(2,1),(3,1),(4,2)] |
| 5 | [(3,1),(4,2),(5,2)] | [(1,0),(2,1),(3,1),(4,2),(5,2)] |
자 이제 조금 익숙해졌을거라고 생각이 된다. 이제 무엇을 봐야할까?
바로 queue에서 추출한 (3,1)이다.
3과 인접한 노드는 무엇인가하니 [1,2,4,6]이다. [1,2,4]는 이미 방문했기에 pass해준다.
6의 경우만 봐주면 된다.
| node | 1 | 2 | 3 | 4 | 5 | 6 |
| visited | T | T | T | T | T | T |
| depth | 0 | 1 | 1 | 2 | 2 | 2 |
| i | queue | result |
| 1 | [(1,0)] | [(1,0)] |
| 2 | [(2,1)] | [(1,0),(2,1)] |
| 3 | [(2,1),(3,1)] | [(1,0),(2,1),(3,1)] |
| 4 | [(3,1),(4,2)] | [(1,0),(2,1),(3,1),(4,2)] |
| 5 | [(3,1),(4,2),(5,2)] | [(1,0),(2,1),(3,1),(4,2),(5,2)] |
| 6 | [(4,2),(5,2),(6,2)] | [(1,0),(2,1),(3,1),(4,2),(5,2),(6,2)] |
자 이렇게 모든 node들을 방문했다.
(남은 queue에서 뽑아도 다 이미 방문했기에 pass된다.)
이때의 result의 (key,depth)를 살펴보면 된다.
최장거리는 2이며 거리가 2인 노드들은 총 3개로 정답은 3이 된다!
여기서 queue가 텅텅 빌 때 까지 수행할수도 있겠지만 visited가 모두 T가 되면 중단시키는 것도 방법이 될 것 같다.
위 프로세스대로 코드를 구현해보자.
import Foundation
func solution(_ n:Int, _ edge:[[Int]]) -> Int {
// 2일 경우 무조건 1개
if n == 2 { return 1 }
// 빈 연결리스트 생성
var nodes = [Int:[Int]]()
// 방문 여부 기록 (F:미방문, T:방문)
var visited = Array(repeating: false, count:n)
// 주어진 정보로 graph 만들기
func connect(key:Int, element:Int) {
if nodes.keys.contains(key) {
nodes[key]?.append(element)
} else {
nodes[key] = [element]
}
}
for e in edge {
// 양방향이기에 0,1 / 1,0 모두 진행
connect(key:e[0], element: e[1])
connect(key:e[1], element: e[0])
}
// (노드,거리) 기록
// queue : FIFO 형태로 인접한 노드를 방문할 수 있도록 해준다.
// result : (노드,거리)를 계속 누적해가며 경우의 수를 모두 저장한다.
var queue = [(Int,Int)]()
var result = [(Int,Int)]()
// key : 현재 방문 지점
// nodes[key]! : 인접 지점 리스트
// depth : 출발점과의 거리
func bfs(key: Int, depth: Int) {
for node in nodes[key]! {
// 들렸던 곳은 패스
if visited[node-1] {
continue
}
// 안들린 곳만 진행
// 방문 기록 남기기
visited[node-1] = true
// 인접점 이동을 위해, 결과값 저장을 위해 append
queue.append((node,depth))
result.append((node,depth))
}
}
// 초기화 : 1에서 출발하기 때문
queue.append((1,0))
visited[0] = true
// FIFO (First-In-First-Out)
while !queue.isEmpty {
let point = queue.removeFirst()
// 인접점으로 이동할 수록 거리는 1씩 추가
bfs(key: point.0, depth: point.1+1)
}
// 결과값 내 최대 거리를 저장
let maxNum = result.map {$1}.max()!
// "최대 거리 = 결과값 내의 거리"인 지점들을 세준다.
return result.filter {$0.1 == maxNum}.count
}
[ 프로세스 ]
* 위 설명으로 생략
이 문제를 풀고 케이스를 직접 작성해보니 BFS에 대해서 어느정도 이해가 된듯하다. 이제 DFS, 다익스트라, 벨만포드, 크루스칼도 공부해보자..! 그래프들을 하나하나 공부하다보면 점점 이해속도도 빨라질거라 생각이 된다!