[프로그래머스] 후보키 (with Combination)

https://programmers.co.kr/learn/courses/30/lessons/42890

코딩테스트 연습 - 후보키

 

우선 swift에는 combination 내장함수가 없다... 

최근에 Swift Algorithm이라고 해서 패키지가 나왔다고는 하지만 코테 환경에서는 사용이 어려운 것 같다. 

파이썬은 있던데... 아쉽지만 이번 기회에 combiantion을 구현해보게 되었으니 좋은게 좋은거지 싶다!🤓

 

func combinations<T>(_ elements: [T], _ k: Int) -> [[T]] {
    // 배열과 추출 개수가 같을 경우 > 그대로 반환
    if elements.count == k {
        return [elements]
    }
    // 추출 개수가 0인 경우 > 빈 배열 반환
    if k == 0 {
        return []
    }
    // 추출 개수가 1인 경우 > 배열의 각 원소들 반환
    if k == 1 {
        return elements.map {[$0]}
    }
    
    // 결과를 저장할 2차원 배열을 생성한다. 
    var result = [[T]]()
    // 원배열의 첫 원소를 제외한 나머지 배열을 저장한다.
    let rest = Array(elements.suffix(from:1))
    // 나머지 배열들을 이용해서 재귀적으로 조합을 구한다. 
    let subcombos = combinations(rest,k-1)
    // 첫 원소 + 나머지 배열들의 재귀적 조합 결과를 하나씩 붙여서 결과에 더한다.
    result += subcombos.map { [elements[0]] + $0 }
    // 첫 원소와 무관하게 나머지 배열들로만 다시 조합을 구해 결과에 더한다. 
    result += combinations(rest,k)
    
    return result
}

 

우선 다양한 데이터 타입으로 구성된 배열을 수용해주기 위해 제네릭 타입을 이용해 함수를 구현한다. 

재귀적으로 풀어낼 예정이기에, 예외 케이스들의 조건을 앞에 먼저 적어주어 추후 탈출할 수 있도록 해준다. 

 

그 이후에는 재귀적인 개념으로 반복된다고 보면 된다. 

 

사실 이 코드를 처음보면 읭? 할 수도 있다. 

일부 케이스에 대한 진행 과정을 그림으로 봐보자!

(파워포인트 말고 도형 그리기 좋은 툴이 있다면 알려주세요... 피피티 지옥..)

 

[1,2,3,4]의 배열에서 3개를 뽑아 조합을 만들고자 한다.

눈으로 딱 봤을 때, [1,2,3],[1,2,4],[1,3,4],[2,3,4] 총 4개가 바로 보인다.

과연 재귀로 풀었을 때는 어떤식으로 전개되는지 위 코드를 그림으로 이해해보자. 

 

combination 1

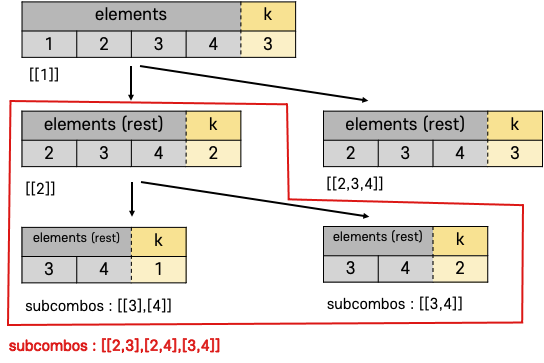
빨간 박스를 보면 k가 1인 경우, elements.count == k인 경우가 있어 재귀가 종료되는 지점이다. 

그 때의 subcombos를 보면 [3],[4],[3,4] 으로 확인이 되나 [3], [4]의 경우는 이전 elements의 첫 원소인 2와 합쳐서 반환해줘야 한다.

그리하여 subcombos를 도출할 수 있다. 

 

그리고 다시 거슬러 올라가보면, 다시 또 이전 elements의 첫 원소를 붙여줘야하고, 우측에 빠져있는 부분은 바로 완성이 되어 result에 추가하여 반환해주면 된다. 

combination 2

 

이렇게 조합이 완성이 되는 것이다. 

그림으로 보니 조금이나마 더 직관적으로 이해할 수 있는 것 같다. 

재귀는.. 머리로 모든 경우를 알 수 없으니 몇 뎁스만 보고 이해하는게 좋을 것 같다!

 

아무튼 이제 조합을 사용해서 본 문제를 풀어볼 것이다. 

 

우선 "후보키"가 되기 위해서는 다음 두 조건이 성립해야 한다.

• 유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
  • ex. 릴레이션의 길이와 후보키로 인덱싱한 데이터의 길이가 같아야 한다. 
• 최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
  • ex. [0]이 키일 경우 [0,1]은 [0]의 상위 집합(superset)이기에 제외되어야 한다. 

 

코드에서 유일성과 최소성을 어떻게 검사하는지 바로 봐보자.

 

import Foundation

func solution(_ relation:[[String]]) -> Int {
    // 열의 개수 = 카테고리 수
    var colCnt = relation[0].count
    
    if colCnt == 1 { return 1 }
    
    var columns = Array<Int>(0..<colCnt)
    var candidateList = [[Int]]()
    
    // 조합 생성
    for i in 1...colCnt {
        candidateList += combinations(columns,i)
    }
    
    // 최종 결과 저장을 위한 키 배열
    var keyList = [[Int]]()
    
    // 조합을 하나씩 돌며
    for candi in candidateList {
        // 중복없는 set 생성
        let candiSet = Set(candi)
        var state = false
        
        // 최소성 체크
        for k in keyList {
            if candiSet.isSuperset(of:k) {
                state = true
                break
            }
        }
        
        // 최소성 조건 미충족시 다음 케이스로 넘어가기 위함
        if state == true {
            continue
        }
        
        // 유일성 체크를 위해 후보키로 인덱싱한 데이터를 구해야한다.
        // 데이터 저장을 위한 배열
        var result = [[String]]()
        
        // 1. 데이터들을 돌며 
        for rel in relation {
            var temp = [String]()
            // 2. 원하는 인덱스의 값을 추가해준다. 
            for c in candi {
                temp.append(rel[c])
            }         
            
            // 3. 중복되지 않는 경우에만 데이터셋에 추가 
            if !result.contains(temp) {
                result.append(temp)
            } else {
                break
            }
        }
        // 유일성 체크 ( 내가 골라낸 유니크한 데이터의 개수와 기존 행 개수가 같아야 조건 충족)
        if result.count == relation.count {
            keyList.append(candi)
        }
    }
    return keyList.count
}

//n개중 m를 순서에 상관없이 뽑아야할 조합들을 만들어주는 함수
func combinations<T>(_ elements: [T], _ k: Int) -> [[T]] {
    // 배열과 추출 개수가 같을 경우 > 그대로 반환
    if elements.count == k {
        return [elements]
    }
    // 추출 개수가 0인 경우 > 빈 배열 반환
    if k == 0 {
        return []
    }
    // 추출 개수가 1인 경우 > 배열의 각 원소들 반환
    if k == 1 {
        return elements.map {[$0]}
    }
    
    // 결과를 저장할 2차원 배열을 생성한다. 
    var result = [[T]]()
    // 원배열의 첫 원소를 제외한 나머지 배열을 저장한다.
    let rest = Array(elements.suffix(from:1))
    // 나머지 배열들을 이용해서 재귀적으로 조합을 구한다. 
    let subcombos = combinations(rest,k-1)
    // 첫 원소 + 나머지 배열들의 재귀적 조합 결과를 하나씩 붙여서 결과에 더한다.
    result += subcombos.map { [elements[0]] + $0 }
    // 첫 원소와 무관하게 나머지 배열들로만 다시 조합을 구해 결과에 더한다. 
    result += combinations(rest,k)
    
    return result
}

 

최소성을 먼저 체크해줌으로써, 먼저 사용 가능한 키인지 확인해준다. 그 이후 해당 키들로 데이터를 선택하여 유일성을 판단해준다. 

유일성까지 충족할 경우 그 때 최종 키 배열에 추가해주는 것이다. 

 

자세한 프로세스는 주석을 따라가보면 이해가 쉬울 것 이다!

 

---

유일성과 최소성이라는 개념에 대해 빠르게 이해하는게 문제를 빠르게 풀 수 있는 키 포인트였던 것 같다. 

유일성은 말 그대로 해당 키로만 비교해도 데이터를 구분할 수 있어야 한다. 즉 키로 추출(인덱싱)한 데이터들이 unique한지를 판단하는 것이 중요한 것이었다. 

가능한 키가 [0] [0,1]로 두 개인데 구분하는데 있어 핵심이 되는 키가 [0]일 경우 [1]은 굳이 필요 없기에 [0]만 키에 저장하는 이러한 과정이 최소성을 충족시키는 과정이다. 이 과정에서 isSuperset라는 메서드를 통해 상위 집합(superset)인지 확인하는 부분은 subset으로도 대체 될 수 있을 것 같다. 

 

끝