[프로그래머스] 가장 큰 정사각형 찾기

https://programmers.co.kr/learn/courses/30/lessons/12905?language=swift 

코딩테스트 연습 - 가장 큰 정사각형 찾기

 

행렬을 받고 가장 큰 정사각형을 만들 때 그 넓이가 얼마가 되는지 구하는 문제이다. 

 

음... 문제를 읽다보니 어디서 본 것 같은 느낌이 든다.. 

 

Count Square Submatrices with All Ones

Count Square Submatrices with All Ones - LeetCode

(?)

 

거의 똑같은 문제!

풀이도 거의 똑같게 해보니 그대로 풀리더라!

 

문제를 푸는 방식은 다음과 같다. 

 

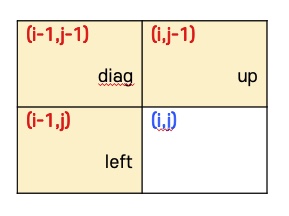
우선 가장 작은 정사각형 형태로 탐색을 해본다고 가정하면 위처럼 index 번호를 매겨줄 수 있다. 

기준이되는 (i,j)의 주변 3개의 값들을 먼저 보고 기준과 비교해봄으로써 정사각형이 될 수 있는지 보는 것이다. 

 

예시를 들어서 봐보자.

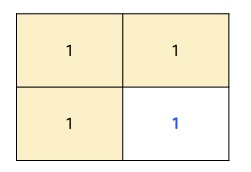
1. diag와 up을 비교한다. (최솟값 : 1)

2. 1번의 최솟값과 left를 비교한다 (최솟값: 1)

3. 주변값들의 최솟값은 현재 1이다. 그리고 이를 기준과 비교하여 최솟값을 구하면 그대로 1이 나온다. 

4. 즉 모두 1이라는 의미가 되고, 이는 곧 2x2 정사각형을 만들 수 있다는 것을 의미한다. 

5. 이 정보를 (i,j)에 표기해주고자 최솟값(diag,left,up의)에 +1을 해준다!

 

그러면 다음과 같이 (i,j)는 2로 값이 바뀌게 된다. 

반면에 한 군데라도 0이 껴있으면 어떻게 될까?

앞선 최솟값을 구하는 1,2번 과정에서 0이라는 값이 최솟값이 되어 기준과 비교를 하여도 0이된다. 

즉 정사각형을 만들 수 없다라는 의미가 된다. 그렇게 이 케이스는 패스해주면 된다. 

 

이렇게 하나하나 행렬을 돌면서 확인을 하게 되면 다음과 같은 구성도 마주하게 될 수 있다.

주변부 값들이 모두 2인 경우이다. 이 때 최솟값은 2로 넘어오게 되고, 이를 기준값과 비교하면 최솟값은 1이 된다.

여기서 이해가 잘 안 갈 수 있는데, 다시 봐보자. 

2라는 값을 가지고 있다는 것 자체가 해당 index를 기준으로 diag,left,up 방향으로 2x2 정사각형을 만들 수 있다는 말이다. 

즉 실제 판단할 때는 빨간 박스, 초록 박스, 파란 박스의 모든 부분을 보지 않지만 그 정보를 갖고 있는 (i,j)로 판단하게 되는 것이다.

그래서 아래와 같이 값을 변경하여 총 3x3의 정사각형을 만들 수 있다고 표기해주어야 한다. 

감이 조금씩 오나요...?

 

4개의 최솟값이 0이 아니라면 min(주변부) + 1  정사각형을 만들 수 있는 것이기에 (i,j)에 min(주변부) + 1의 값을 할당해주는 것이다!

 

이제 코드로 보는게 이해가 빠를 것이다. 

 

import Foundation

func solution(_ board: [[Int]]) -> Int {
    // board 복사 (값 변경을 위해!)
    var board = board
    
    // 행
    for i in 1..<board.count {
        // 열
        for j in 1..<board[0].count {
            // 위의 원소 
            let up = board[i][j-1]
            // 왼쪽 원소
            let left = board[i-1][j]
            // 대각 왼쪽 위 원소 
            let diag = board[i-1][j-1]
            // 3개 값 중 최솟값을 구해서
            let minval = min(up,min(left,diag))
            // 기준값과 다시 비교해서 최솟값을 구했을 때 0이 나오면 정사각형은 못만드는 것
            // 1이나 다른 값이 나왔다면 만들 수 있다는 것 
            if min(board[i][j], minval) == 0 {
                continue
            } else {
                // 만들 수 있는 경우이기에 기준에 +1을 해줘서 정사각형의 크기를 채워나간다
                board[i][j] = minval + 1
            }
        } 
    }

    // 최대 크기 구하기
    let rect = board.flatMap {$0}.max()!
    return rect * rect
}

 

마지막에 넓이를 구하기 위해 최대 정사각형의 길이를 얻어내는 부분만 제외하면 모든 부분을 위에서 설명한 셈이다.

최솟값으로 비교하여 행렬 내에서 가장 큰 정사각형의 크기를 구하는 DP같은(?) 문제였던 것 같다. 

 

끄읕