이전에 포워딩 테이블은 라우팅 알고리즘에 의해서 만들어진다고 했었다.
이번 강의에서는 라우팅 알고리즘에 대해서 알아볼 것이다.
Routing Algorithms
라우터의 주 역할 중 하나는 포워딩이었다. 포워딩이라는 것은 패킷 내 헤더의 목적지 정보를 보고 포워딩 테이블내 가장 적합한 엔트리와 매칭해서 연결시켜주는 것이다. 즉 A를 B로 보내기 위해 중간에 거쳐야하는 관문 정도로 보면 될 것 같다.
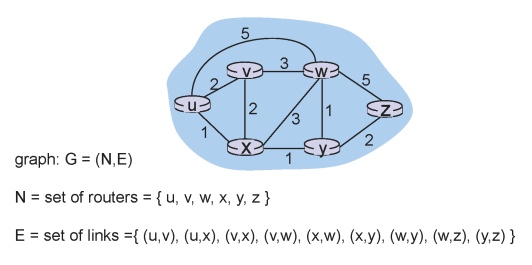
이제는 네트워크를 그림으로만 보지 않고 노드와 간선으로 이루어진 네트워크 그래프로 볼 것이다.
노드는 라우터고, 간선은 링크라고 보면 된다.
이 네트워크 그래프를 보는 이유가 뭘까??
바로 앞서 말했듯이 포워딩 테이블을 만들기 위해서이다.
어? 그럼 포워딩 테이블의 엔트리는 어떻게 구성해야 좋은거지??
예를 들어, 위 그림에서 라우터 u가 라우터 z와 연결하려고 한다면 다양한 경로를 거칠 수 있을 것이다.
그 중에서 두 가지 경로만 놓고봐보자.
u -> v -> w-> z // 총 비용 : 10
u -> x -> y -> z // 총 비용 : 3
위 두 가지 경로 중에서 어떤 걸 택해서 포워딩 테이블에 적으면 좋을까?
바로 목적지로 가는 경로 중 최소 비용인 경우를 포워딩 테이블에 저장해주면 되는 것이다.
즉, 여러 알고리즘 문제를 풀 때 봤던 최단 경로를 구하는 것과 동일한 문제가 된다.
이러한 포워딩 테이블을 구하기 위해 어떠한 알고리즘을 사용할 지 선택해야하는데, 그래프의 현재 상황에 따라 그 방법이 다르다.
현재 상황..? 그건 또 무슨 말...
현재 상황이라고 하면 크게 두 가지(global/decentralized)로 나눌 수 있다.
- Global
- 모든 라우터가 각각이 연결된 비용을 알고 있을 때 (= 라우터가 그래프 상 모든 간선의 비용을 알 때)
- 이 상황에서는 link state 알고리즘
- Decentralized
- 라우터가 물리적으로 인접한 이웃 라우터에 대한 비용만 알고 있을 때
- 이 경우, 반복적으로 인접한 라우터를 방문하며 최소 비용을 구해나갈 수 있다.
- 이 상황에서는 distance vector 알고리즘
이번 강의에서는 link state 알고리즘에 대해서 살펴보자!
Link State Routing Algorithm
link state의 대표적인 알고리즘은 "다익스트라 알고리즘"이다.
그래프내 모든 간선의 비용을 알고 있고, 한 지점에서 다른 지점들까지의 최소 비용을 구하기 위해 사용되는 방식이다.
pseudo code를 먼저 봐보자.

우선 간략하게 말하면 아래와 같다.
1. N'은 최소 비용이 확정된 것이다. (이후 점점 확장되며 N'가 전체와 같아지면 종료된다)
2. 우선 모든 노드들에 대해 인접한 노드들과의 비용 정보를 통해 연결하고, 연결되어 있지 않다면 Inf 값을 넣어준다.
3. 시작점에서 인접한 노드들에 대해 최소 비용으로의 간선을 구성한다.
4. 최소 비용을 구했다면 N'에 추가!
u 노드를 기준으로 보면 v,w,x,y,z는 모두 잠재적인 목적지가 될 수 있다. 그렇기에 우선은 인접노드들 뿐만 아니라 전체 노드들에 대해 정보를 입력해준다.
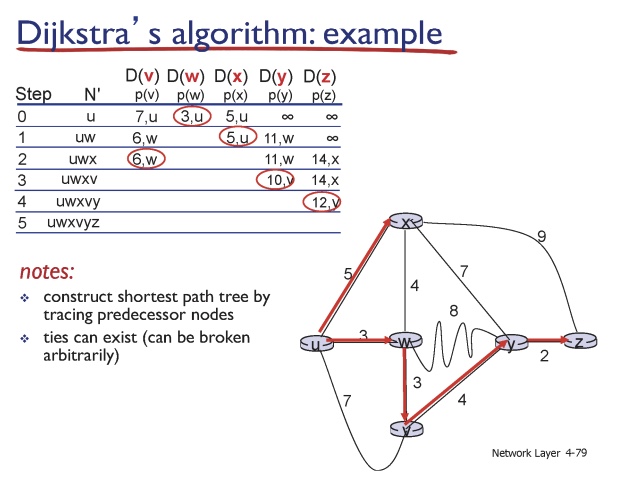
Step 0
u와 인접한 x,w,v에 대해서는 정확한 값을 적어줄 수 있다. v까지의 거리를 D(v)라고 나타낸다.
step0의 표를 살펴보면 여기서 가장 최소의 값은 (u -> w, 3) 이다.
Step 1
이제 w는 최소값으로 구해졌기 때문에 다른 노드들을 살펴본다. w에서 v로 가는 경우를 살펴보면 3이고 기존의 값을 더하면 6이 되어서 step 0에서 구한 경로보다 더 비용이 저렴하게 된다. 이런 경우를 찾아가며 계속 업데이트 하는 것이다.
그렇게 쭉쭉 반복하다보면 결국 u에서 z까지 이동하는데 최소 비용은 12인 것이다.
하지만 어떻게 전체 네트워크들과의 연결 비용을 알 수 있을까??
원래는 브로드캐스트를 통해 그래프를 그릴 수 있는데 전세계 인터넷과 브로드캐스트 할 수 있을까??
이는 사실 불가하다. 그렇기 때문에 동일한 도메인에 속하는 네트워크(관리 주체가 같은)들에 대해서만 라우팅 알고리즘을 사용한다. 예를 들어 A 네트워크, B 네트워크, C 네트워크가 있다면 A-B-C 간에 link state 알고리즘을 사용하는 것이 아니라 A 내에서 link state 알고리즘을 사용한다고 이해하면 될 것 같다. A-B-C 사이, 즉 외부끼리 연결하는 것은 또 다른 방법을 사용한다고 한다.
Distance vector algorithm
distance vector 알고리즘에 대해 살짝 알아보자.
앞서 말했던 것과 같이, 전체 그래프의 정보를 아는 것이 아니고 인접한 부분에 대해서만 알고 있기 때문에 아래와 같이 최소 비용을 구할 수 있다.
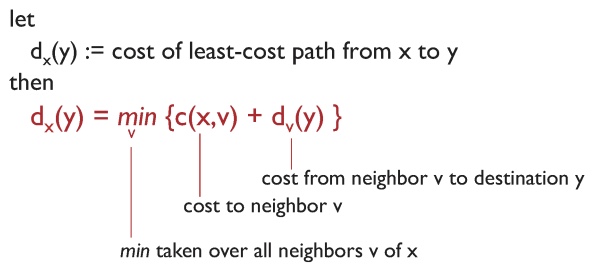
식을 간단하게 말해보자면 "주변부까지 거리 + 주변부에서 목적지까지 비용"을 구하는 것이다. 살펴보면 v에서 y로 가는 부분은 다시 위 식을 반복하는, 즉 재귀 형태로 진행이 된다. 주변부의 값만 알고 있기 때문에, 우선은 확실한 인접 부분에 대한 비용을 더하고 나머지는 반복하며 알아내는 방식인 것이다!
자세한건 다음 강의에서!
![[Network] 네트워크 계층 4](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FuAO9A%2FbtreotClgnL%2FkYpV8VkEtXynJuxwPxuCp1%2Fimg.jpg)